Elevando a potenza con ESPONENTE INTERO POSITIVO _ i due membri di una disuguaglianza fra NUMERI NEGATIVI
si ottiene una disuguaglianza dello STESSO SENSO se l'esponente è DISPARI
e di SENSO CONTRARIO se l'esponente è PARI
Se a e b sono numeri NEGATIVI e n un numero intero POSITIVO DISPARI _ tali che a > b sarà anche:
a
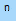 > b
> b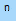
quindi il senso rimane invariato.
Se invece n è un numero intero POSITIVO PARI sarà :
a
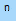 < b
< b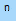
quindi il senso si inverte.
Esempio: Data la disuguaglianza: -3 > -6
elevando al cubo esponente dispari si ottiene:
- 27 > -216 quindi il senso rimane invariato
Elevando al quadrato esponente pari si ha:
9 < 36 cioè il senso si inverte.
Si noti che elevando a potenza con esponente positivo _ i membri di una disuguaglianza tra numeri di segno opposto
non è possibile determinare a priori il senso della disuguaglianza risultante infatti:
nell'ipotesi di n = 2 si può avere:
1 da 3 > -3 elevando al quadrato si ottiene un'identità: 9 = 9;
2 da 7 > -2 si ottiene una disuguaglianza con lo stesso senso: 49 > 4
3 da 5 > -8 si ottiene una disuguaglianza con senso contrario: 25 < 64.