Sintesi delle derivate più comuni
Derivata di una costante

y = costante      y' = 0
la derivata della funzione ipsilon = costante è uguale a 0
Derivata di: y = x
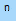
y = x 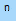      y' = nx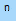
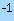
la derivata di ics elevata alla enne è uguale a n per ics elevata alla enne meno uno
Derivata di: y = x
Derivata della funzione y uguale a ics y = x       y' = 1
la derivata della variabile indipendente x è uguale a 1
Derivata di: y =
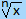
Derivata della funzione radice ennesima di ics y =      
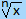
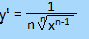
la derivata della radice ennesima di ics è uguale a uno fratto enne per radice ennesima di ics alla enne meno uno
Derivata di senx
Derivata della funzione: seno di ics y = senx       y' = cosx
La derivata della funzione: senx è uguale a cosx
Derivata di cosx
Derivata della funzione: coseno di ics y = cosx       y' = - senx
La derivata di cosx è uguale a meno senx
Derivata di tgx
Derivata della funzione: tangente di ics /                                                    1

y = tgx                      y' = ------------- = 1 + tg²x

                                            cos² x
La derivata di tangente di ics è uguale a uno fratto coseno al quadrato di ics ovvero a uno più tangente al quadrato di ics
Derivata di cotgx
Derivata della funzione: cotangente di ics /                                                    1

y = cotgx                      y' = ------------- = - (1 + cotg²x )

                                            sen² x
La derivata di cotangente di ics è uguale a uno fratto seno al quadrato di ics ovvero a uno più cotangente al quadrato di ics
Derivata di a
Derivata della funzione: a alla ics a       y' = a lg a
La Derivata di a alla ics è uguale ad a elevata alla ics per logaritmo di a
Derivata di e
Derivata della funzione: e alla ics e       y' = e
La Derivata di e alla ics è uguale ad e elevata alla ics