o di Lagrange o di Cavalieri
Data una funzione y = f(x), continua nell’intervallo chiuso e limitato [a,b]
e derivabile nell’intervallo aperto (a,b) ,
esiste almeno un punto c ∈ (a,b), tale che risulti:
f(b)-f(a)
f'(c) = ----------------
b-a
Geometricamente significa che, esiste un punto c ∈ (a,b),
in cui, la tangente è parallela alla secante.
Dimostrazione
Si consideri la funzione f(x) avente il grafico:
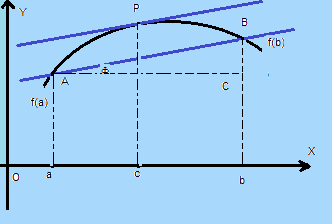
Si consideri l'arco AB, e la relativa corda.
E' intuitivo che, sull'arco AB, ci sarà almeno un punto
in cui, la tangente alla curva, sarà parallela alla corda AB
Si tracci, da A, la parallela all'asse x, e si consideri il segmento AC
risulta: AC = b - a, e BC = f(b) - f(a)
Essendo il triangolo ACB, rettangolo si può scrivere:
BC f(b) - f(a)
tgφ = ---- = ----------
AC b - a
L'angolo φ è anche l'angolo che la tangente alla curva in P, forma con l'asse x
pertanto tgφ è anche il suo coefficiente angolare
Si può, quindi, scrivere tgφ = f'(c),(per il significato geometrico della derivata).
Per definizione, si può scrivere anche:
f(b) - f(a)
--------- = f '(c)
b - a
da cui si estrae l'enunciato del teorema:
f(b) - f(a) = (b - a) f'(c).