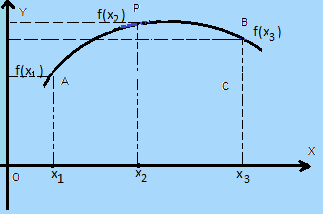
Si definisce campo di esistenza di una funzione
l'insieme dei valori che si possono attribuire alla x variabile indipendente
perchÚ esista il corrispondente valore della y variabile dipendente
Infatti non sempre Ŕ possibile attribuire alla x qualunque valore
ad esempio se la x rappresenta un lato di una figura geomÚtrica
non Ŕ possibile attribuire ad essa valori negativi
Esempio: Data la funzione
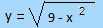
PerchŔ la y assuma valori reali Ŕ necessario che la x non assuma mai valori positivi maggiori di 3
e neppure valori negativi minori di -3
altrimenti avremmo la radice quadrata di un numero negativo
Quindi il suo campo di esistenza sarÓ -3 ≤ x ≤ 3