se il limite di una funzione f(X), per X → Xo,
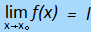
esiste,se, il limite di una funzione effe di ics, per ics tendente a ics con zero, esiste
allora esso è unico.
Dimostrazione
Se f(X) per X che tende a Xo avesse due limiti diversi l e l1
l-l1
posto: ε= -----,
2
si potrebbe trovare un intorno γ1 e un intorno γ2 di Xo
per cui valessero le relazioni:
|l-l1|
|f(X) - l| < ----,
2
|l-l1|
|f(X) - l1| < ----,
2
in un intorno di Xo contenuto in γ1 e γ2 le due relazioni appena scritte varrebbero entrambe
sommandole membro a membro:
|f(X) - l|+ |f(X) - l1| < |l-l1|
Poiché il valore assoluto della differenza di due numeri relativi
non supera mai la somma dei valori assoluti degli stessi, risulta:
|[f(X)- l1]-[f(X)-l]|<=|f(X)-l1| + |f(X)-l|
a maggior ragione si ha:
|[f(X)- l1]-[f(X)-l]|< |l-l1|
ovvero: |l-l1|<|l-l1|
che è assurdo,
per cui f(X) non può avere due limiti per X che tende a Xo.