La derivata prima di una funzione f(x) relativa ad un suo punto di ascissa Xo
è il limite, se esiste ed è finito, del rapporto incrementale,
al tendere a zero dell'incremento h cioè:
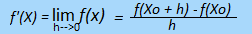 Si rappresenta sinteticamente, con i simboli f'(x) oppure y' oppure D[f(x)]
Si rappresenta sinteticamente, con i simboli f'(x) oppure y' oppure D[f(x)]e corrisponde al coefficiente angolare della retta tangente al grafico della funzione ƒ(X)nel punto di ascissa (Xo ƒ(Xo)).
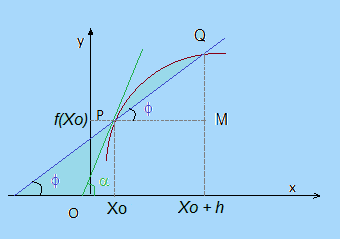 Dal grafico si comprende che, quando h tende a 0, X0 + h diventa X0, e il punto Q va a sovrapporsi al punto P
Dal grafico si comprende che, quando h tende a 0, X0 + h diventa X0, e il punto Q va a sovrapporsi al punto PPer cui, la retta bleu si inclina sempre di più, fino a sovrapporsi
e quindi a coincidere con la retta verde,
che non è altro che, la tangente alla funzione f(x) nel punto P(Xo,f(Xo)).